Graph and UnDirected Graph
Graph
Generally, graphs can be catergorized as undirected graph and directed graph, in this chapter, we use unweighted undirected graph to illustrate most cases. :)
Construction: Adjacency List and Adjacency Matrix
public static class IndirectGraph{
private static int numVertex;
private static ArrayList<Integer>[] adjList;
private static boolean[][] adjMatrix;
public IndirectGraph(int numVertex) {
this.numVertex = numVertex;
adjMatrix = new boolean[numVertex][numVertex];
adjList = new ArrayList[numVertex];
for (int i=0; i<numVertex; i++){
adjList[i] = new ArrayList<>();
}
}
public static void addEdge(char c1, char c2){
int v1 = c1 - 'A';
int v2 = c2 - 'A';
adjList[v1].add(v2);
adjList[v2].add(v1);
adjMatrix[v1][v2] = true;
adjMatrix[v2][v1] = true;
}
public static void printAdjList(){
System.out.println("Indirect Graph Adjacency List: ");
for (int i=0; i<numVertex; i++){
System.out.print("\n"+(char) ('A' + i)+": ");
for (int j=0; j<adjList[i].size(); j++){
System.out.print((char) ('A'+adjList[i].get(j))+" ");
}
}
}
public static void printAdjMatrix(){
System.out.println("\nIndirect Graph Adjacency Matrix: ");
for (int i=0; i<numVertex; i++){
System.out.print("\n"+(char) ('A' + i) + ": ");
for (int j=0; j<numVertex; j++){
System.out.print(adjMatrix[i][j]? "1 " : "0 ");
}
}
}
}
This is the graph we use:
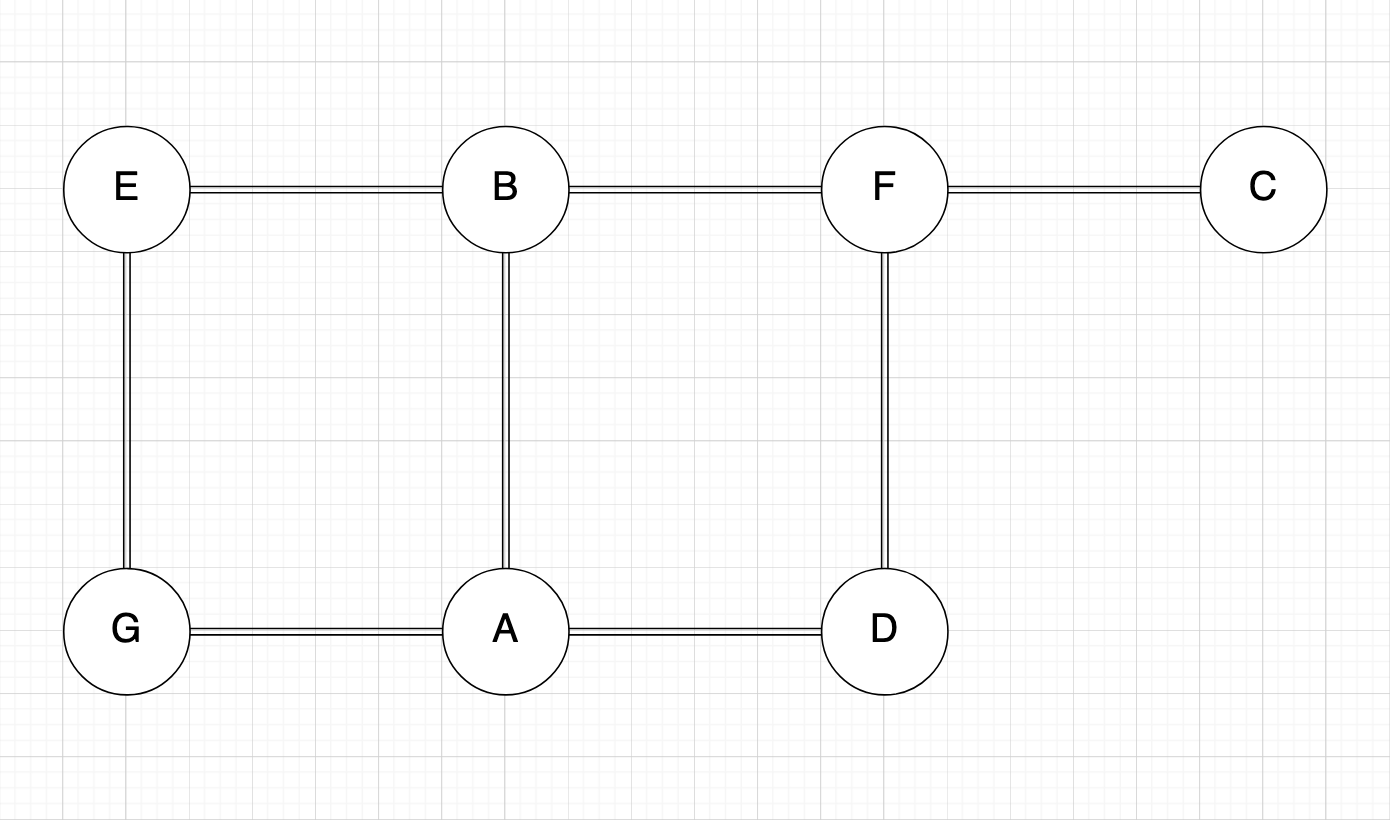
power by draw.io :)
construction code:
public static void main(String [] args){
IndirectGraph indirectGraph = new IndirectGraph(7);
[E]--------[B]--------[F]--------[C]
| | |
| | |
| | |
[G]--------[A]--------[D]
indirectGraph.addEdge('A', 'B');
indirectGraph.addEdge('A', 'D');
indirectGraph.addEdge('A', 'G');
indirectGraph.addEdge('B', 'E');
indirectGraph.addEdge('B', 'F');
indirectGraph.addEdge('C', 'F');
indirectGraph.addEdge('D', 'F');
indirectGraph.addEdge('E', 'G');
indirectGraph.printAdjList();
indirectGraph.printAdjMatrix();
}
BFS: Breadth First Search
public static void BFS(IndirectGraph graph, char start){
//initialized to be false
boolean [] visited = new boolean[graph.numVertex];
//FIFO
Queue<Integer> queue = new LinkedList<>();
//add the next vertex(-ices) to visit in queue, in this case, 'A'
visited[start - 'A'] = true;
queue.add((int)start);
while (!queue.isEmpty()){
//(iteratively) read element(s) from the queue
int vert = queue.poll();
System.out.print( (char)vert + " ");
//use adjacency list
for (int i=0; i<graph.adjList[vert - 'A'].size(); i++){
//[vert - 'A'] is the label of each adjList
int num = graph.adjList[vert - 'A'].get(i);
//if it is not visited, add to queue
if(!visited[num]){
visited[num] = true;
queue.add(num+'A');
}
}
}
}
🤔 This block of code could be beutify. In adjList<> and queue<>, values of the some vertex is different.
DFS: Depth First Search
Implementation with Recursion
public static void RecursiveUtilDFS(IndirectGraph graph, char start, boolean[] visited){
visited[start - 'A'] = true;
System.out.print(start + " ");
Iterator<Integer> i = graph.adjList[start - 'A'].listIterator();
while(i.hasNext()){
int n = i.next();
if (!visited[n]) {
RecursiveUtilDFS(graph, (char) (n + 'A'), visited);
}
}
}
public static void RecursiveDFS(IndirectGraph graph, char start){
boolean [] visited = new boolean[graph.numVertex];
RecursiveUtilDFS(graph, start, visited);
}
Implementation with Iteration
public static void DFS(IndirectGraph graph, char start){
boolean [] visited = new boolean[graph.numVertex];
Stack<Integer> stack = new Stack<>();
stack.push((int)start);
while(!stack.isEmpty()){
int vert = stack.pop();
if(!visited[vert-'A']){
visited[vert-'A'] = true;
System.out.print((char) vert + " ");
for (int i=0; i<graph.adjList[vert-'A'].size(); i++){
int neighbor = graph.adjList[vert-'A'].get(i);
if(!visited[neighbor]){
stack.push(neighbor+'A');
}
}
}
}
}
Shortest Path on UDG (UnDirected Graph)
The shortest path algorithm is a fundamental concept in graph theory that finds the most efficient route between two nodes in a graph. It has numerous applications, including navigation systems, network routing protocols, and resource allocation problems. The importance of this algorithm lies in its ability to solve optimization problems that involve finding the path with minimum cost or distance. By minimizing the number of steps or distance traveled, the algorithm can save time and resources. The shortest path algorithm is widely used in computer science, operations research, and transportation engineering.
To illustrate our algorithms, we need a weighted UDG:
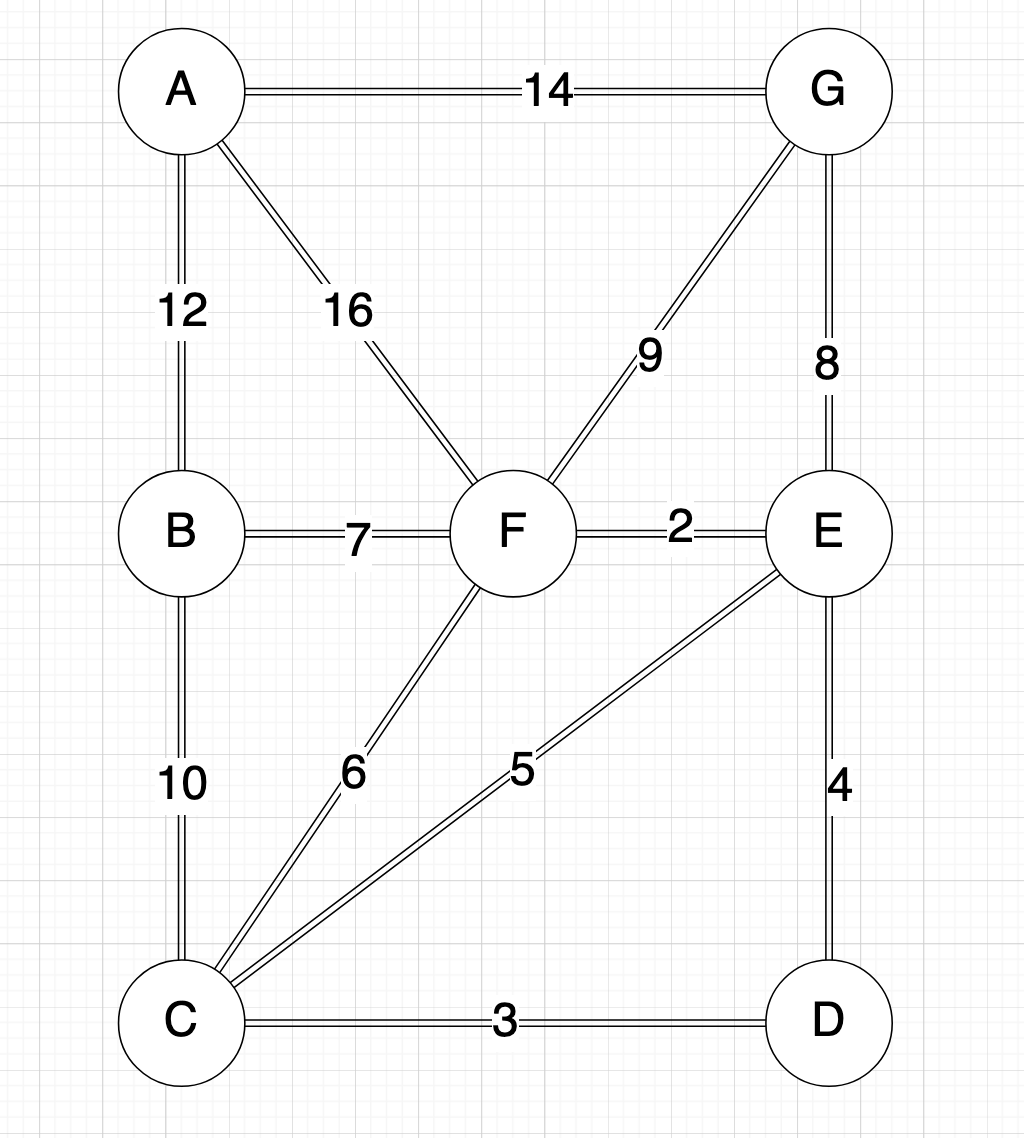
powerer by draw.io :)
Weighted UDG
public static void main(String [] args){
A B C D E F G
A { 0, 12, INF, INF, INF, 16, 14}
B { 12, 0, 10, INF, INF, 7, INF}
C { INF, 10, 0, 3, 5, 6, INF}
D { INF, INF, 3, 0, 4, INF, INF}
E { INF, INF, 5, 4, 0, 2, 8}
F { 16, 7, 6, INF, 2, 0, 9}
G { 14, INF, INF, INF, 8, 9, 0}
WeightedUDG wUDG = new WeightedUDG(7);
wUDG.addWeight(0,1,12);
wUDG.addWeight(1,2,10);
wUDG.addWeight(2, 3, 3);
wUDG.addWeight(2, 4, 5);
wUDG.addWeight(3, 4, 4);
wUDG.addWeight(0, 5, 16);
wUDG.addWeight(1, 5, 7);
wUDG.addWeight(2, 5, 6);
wUDG.addWeight(4 ,5, 2);
wUDG.addWeight(0, 6, 14);
wUDG.addWeight(4, 6, 8);
wUDG.addWeight(5, 6, 9);
int [][] graph = wUDG.getWeightedUDG();
int [] dist = DijkstraAlg(graph, 0);
System.out.println(Arrays.toString(dist));
}
public static class WeightedUDG{
private static int numVert;
private static int [][] weightedUDG;
public WeightedUDG(int numVert){
numVert = numVert;
weightedUDG = new int[numVert][numVert];
for (int i=0; i<numVert; i++){
Arrays.fill(weightedUDG[i], Integer.MAX_VALUE);
}
for (int i=0; i<numVert; i++){
weightedUDG[i][i] = 0;
}
}
public static void addWeight(int vert1, int vert2, int weight){
//index starts from 0
//by default, the path to itself is zero
if(vert1 != vert2){
weightedUDG[vert1][vert2] = weight;
weightedUDG[vert2][vert1] = weight;
}
}
public static int[][] getWeightedUDG(){
return weightedUDG;
}
}
Vanilla Dijkstra Algorithm
public static int [] Dijkstra(int [][]graph, char _start){
int start = _start-'A';
boolean [] visited;
int [] distance;
visited = new boolean[graph.length];
distance = new int[graph.length];
Arrays.fill(distance, Integer.MAX_VALUE);
Arrays.fill(visited, false);
distance[start] = 0;
for(int i = 0; i < graph.length - 1; i++){
int minDist = Integer.MAX_VALUE;
int minNode = -1;
for (int j = 0; j < distance.length; j++) {
if (!visited[j] && distance[j] < minDist) {
minDist = distance[j];
minNode = j;
}
}
if (minNode == -1) {
break;
}
int u = minNode;
visited[u] = true;
for (int v=0; v < graph.length; v++){
if(graph[u][v] < Integer.MAX_VALUE && !visited[v] && distance[v] > distance[u] + graph[u][v] ){
distance[v] = distance[u] + graph[u][v];
}
}
}
return distance;
}
Dijkstra Algorithm with Priority Queue
public static int [] DijkstraAlg(int [][] graph, int start){
boolean [] visited;
int [] distance;
int [] prevVert;
PriorityQueue<Integer> pq;
visited = new boolean[graph.length];
distance = new int[graph.length];
prevVert = new int[graph.length];
Arrays.fill(distance, Integer.MAX_VALUE);
Arrays.fill(visited, false);
Arrays.fill(prevVert, -1);
pq = new PriorityQueue<>(graph.length, Comparator.comparingInt(a -> distance[a]));
pq.offer(start);
distance[start] = 0;
while (!pq.isEmpty()){
int u = pq.poll();
visited[u] = true;
for (int v=0; v < graph.length; v++){
if(graph[u][v] < Integer.MAX_VALUE && !visited[v] && distance[v] > distance[u] + graph[u][v] ){
distance[v] = distance[u] + graph[u][v];
pq.offer(v);
}
}
}
return distance;
}